Inhalt
Aufgaben um den Pythagoras
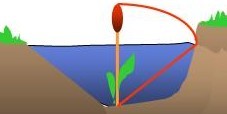
Die folgende Aufgabe soll aus China, 13. Jh. n. Chr. stammen:Fünf Fuß vom Ufer eines Teiches entfernt rage ein Schilfrohr einen Fuß über das Wasser empor. Man ziehe seine Spitze an das Ufer wie in der Abbildung, dann berühre sie gerade den Wasserspiegel.
Wie tief ist der Teich?
52 + t2 = (1 + t)2
52 + t2 = 12 + 2·1·t + t2
Ergibt: t = 12
Aus einem Rechenbuch um 1550:
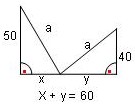
Zwei Türme stehen auf ebenem Felde 60 Ellen voneinander entfernt, einer 50, der
andere 40 Ellen hoch. Zwischen den Türmen steht ein Brunnen, gleich weit weg von
den Spitzen der Türme.
Ist die frag wie fern steht der vnden von yedem Thurn?
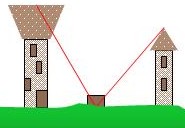
Mit a=a und x+y=60 sowie den Höhen 40 und 50 und den rechten Winkeln haben wir genug
Informationen für diese Gleichungen:
a2 = 502 + x2 und a2 = 402 + y2
Gleichsetzen beider Gleichungen und berücksichtigen von y=60-x liefert
502 + x2 = 402 + (60 - x)2
Das könnt ihr eigentlich selber durchrechnen um zu sehen, dass die Ergebnisse
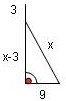
Ein 10 Fuß hoher Baum ist so geknickt, dass seine Spitze 3 Fuß entfernt den Boden berührt. Wie hoch liegt der Bruch?

Wir setzen 32 + x2 = y2 und mit y = 10 - x
32 + x2 = (10 - x)2
Die übliche quadratische Gleichung bei solchen Aufgaben liefert schließlich
4,05 Fuß Höhe für den noch stehenden Baumstumpf und den Rest bis 10 Fuß
für die Krone mit Teilstamm.
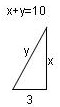
x senkrecht auf 3
Die folgende Aufgabe mit der Leiter oder dem Balken existiert schon in einem
altbabylonischen Text (ca. 2000 v.Chr.) und in einem syrischen Text um 400 v.Chr.,
so und in ähnlicher Form immer wieder.
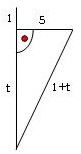
Eine Leiter stehe parallel zu einer Wand und werde 3 Ellen herunter gezogen, dann sei
sie unten 9 Ellen von der Wand entfernt.