Inhalt
Fermat
Für pythagoreische Zahlen gilt
c2 = a2 + b2
da liegt die Vermutung nahe
c3 = a3 + b3
Wohlgemerkt, das Tripel (a,b,c) müsste aus dem Bereich der natürlichen Zahlen kommen.
Geometrisch sähe das so aus, dass das Volumen des Würfels mit der Kantenlänge c so groß wie die Summe der Volumina der Würfel mit den Kantenlängen a und b wäre.
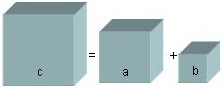
Warum nicht einen Schritt weiter? Vermuten wir mutig
cn = an + bn
wobei n ebenfalls eine natürliche Zahl sein möge. Könnte man das zeichnerisch darstellen
für n>3?
Ob die Pythagoreer daran gedacht haben? Verkneifen wir uns jede Spekulation, wir sind keine Politiker. Generationen von Mathematikern befassten sich mit obigen 2 Gleichungen, das Ergebnis war lange summa summarum erschütternd. Obwohl, es gibt da so eine Geschichte.
Der bedeutende französische Mathematiker Fermat hatte sich eingehend mit einem seiner
großen griechischen Vorgänger, dem Diophantos von Alexandria und dessen Werken befasst.
Dabei soll er in das Buch des Vorgängers an die Randseite geschrieben haben, einen
wunderbaren Beweis gefunden zu haben, dass die Gleichung
Pech auf der ganzen mathematischen Linie?
Inzwischen ist die Angelegenheit erledigt.
Mal abgesehen von pythagoreischen Zahlentripeln und so, aber wenn
c = a + b
Ein ganz böser Fehler, ich mag gar nicht hinsehen!
Macht euch gründlich klar, welcher Fehler hier gemacht wurde, auf dass euch das niemals
passieren möge.