Inhalt
Umkehrungen der Satzgruppe des Pythagoras
Der Satz des Pythagoras kann gut verständlich so lauten:
Wenn Dreiecke rechtwinklig sind, dann ist das Quadrat über der Hypothenuse genauso groß
wie die Summe der Quadrate über den Katheten.
Wir wissen schon: Nach wenn... kommt die Voraussetzung, nach dann... kommt die Behauptung.
Vertauschen wir einfach Voraussetzung und Behauptung, und wir haben einen
anderen mathematischen Satz:
Wenn in Dreiecken das Quadrat über der Hypothenuse genauso groß ist wie die
Summe der Quadrate über den Katheten, dann sind diese Dreiecke rechtwinklig.
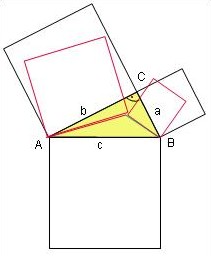 Das Dreieck ABC (rot) sei jetzt stumpfwinklig, dann ist offensichtlich
Das Dreieck ABC (rot) sei jetzt stumpfwinklig, dann ist offensichtlich

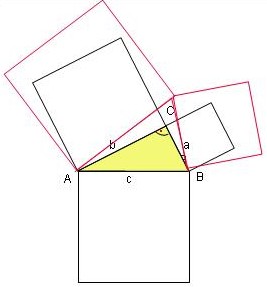 Das Dreieck ABC sei nun spitzwinklig, dann ist offensichtlich
Das Dreieck ABC sei nun spitzwinklig, dann ist offensichtlich
Anwendung der Umkehrung des Satzes des Pythagoras
Im alten Ägypten war es der jährlichen Nilüberschwemmungen wegen notwendig, das Land neu zu vermessen. Dazu verwendete man eine sog. Knotenschnur, in die 12 Knoten im gleichen Abstand geknüft waren. Damit konnte man rechtwinklige Dreiecke abstecken.Erläutere das Verfahren.
Die Umkehrungen zum Höhen- und Kathetensatz findet ihr sicherlich selbst.