Inhalt
Hippokrates
Beinahe lyrisch kommen sie daher, die Möndchen des Hippokrates.
Möndchen und dann noch die zweite Silbe von Hippokrates lang betonen (poo),
das klingt wie sphärische Mathematik.
Stop, etwas Zurückhaltung bitte!
Wir zeichnen einen Halbkreis mit dem Durchmesser c.
Einen Punkt auf der Peripherie verbinden wir mit den Endpunkten des Durchmessers c.
Nach dem Thalessatz haben wir das rechtwinklige Dreieck(a;b;c).
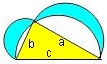
Über a und b zeichnen wir Halbkreise mit den Durchmessern a und b.
Die beiden Kreiszweiecke sind die Möndchen.
Behauptung:
- Flächeninhalt Dreieck = Flächeninhalt(Möndchen1 + Möndchen2)
- gelb = cyan + cyan
Nach Pythagoras sind die Flächeninhalte
Halbkreis über c = Halbkreis (über a + über b)
Auf beiden Seiten voriger Gleichung sind die weißen Kreiszweiecke. Die werden subtrahiert, erledigt.
Wenn das so einfach ist, dann probieren wir es mit einem Quadrat:
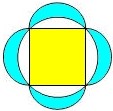
Betrachte das Quadrat als zwei rechtwinklige, gleichschenklige Dreiecke, dann musst du nichts neu berechnen. Also sozusagen
- gelb = 4 · cyan
Eine verlockende Geschichte. Dieser Erkenntnis wegen glaubte schon Hippokrates, der Kreis sei zurückführbar auf das Quadrat, und auch nach ihm versuchten Mathematiker über Jahrhunderte, solchen Beweis zu führen.
Wollen wir heute etwas als unmöglich charakterisieren, dann sprechen wir von der
- Quadratur des Keises.
Hippokrates von Kos (ca. 460-370), griechischer Arzt, Begründer der wissenschaftlichen Medizin der Antike. Auf ihn geht der Eid des Hippokrates zurück, den angehende Mediziner leisten und damit ethische Prinzipien für ihren Berufsstand anerkennen.