Inhalt
Satzgruppe des Pythagoras
Unter der Satzgruppe des Pythagoras versteht man
Satz des Pythagoras
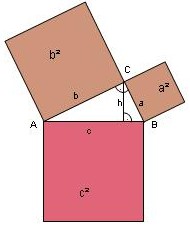
In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypothenuse genauso groß wie die Summe der Quadrate über den Katheten.
Höhensatz
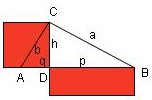
In jedem rechtwinkligen Dreieck ist das Quadrat über der Höhe genauso groß wie das Rechteck aus den beiden Hypothenusenabschnitten
Kathetensatz, Satz des Euklid
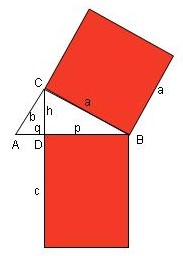
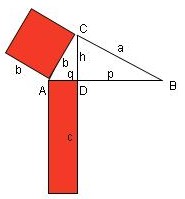
In jedem rechtwinkligen Dreieck ist das Quadrat über einer Kathete genau so groß, wie das Rechteck aus Hypothenuse und zugehörigem Hypothenusenabschnitt
(Zugehöriger Hypothenusenabschnitt ist der, der an der betrachteten Kathete liegt)
Zusammenhang zwischen den Sätzen
Die drei Sätze sind eng miteinander verwandt, so folgtaus dem Kathetensatz der Satz des Pythagoras
aus dem Satz des Pythagoras der Höhensatz
aus dem Höhensatz und dem Satz des Pytahgoras der Kathetensatz.
Begriffe:
(gilt nur für rechtwinklige Dreiecke)
Hypothenuse c:
längste Seite, immer gegenüber dem rechten WinkelKatheten a, b:
die anderen Dreiecksseiten, stehen senkrecht zueinanderHypothenusenabschnitte p, q
p + q = cVoraussetzung:
a ist senkrecht zu b (rechtwinkliges Dreieck)
h ist senkrecht zu c
Die Sätze als Gleichungen:
Pythagoras:
c2 = a2 + b2
Höhensatz:
h2 = p · q
Kathetensatz:
a2 = c · p
b2 = c · q
For pupils only
Natürlich muss man im Fach Mathematik auch auswendig lernen, sonst geht gar nichts. Lernt aber um Gottes Willen nicht die rechts stehenden Gleichungen, lernt die in der Mitte stehenden Sätze. Anderenfalls steht ihr unweigerlich vor einem Problem, wenn die Bezeichnungen der Seiten am Dreieck mal anders aussehen. Glaubt es mir ganz einfach.
Und noch etwas: Beginnt die Sätze nicht mit: In einem rechtwinkligen...
Man könnte euch gleich fragen, wie denn das in anderen rechtwinkligen Dreiecken so ist.