Inhalt
Pythagoreer
Die Zahl sei das Wesen der Dinge, war einer der Grundsätze der Pythagoreer.Die wesentlichen Erkenntnisse zu den Pythagoreern enstammen der wohl mehr erfundenen Pythagoras-Biographie des hellenistischen Mathematikers und Philosophen Iamblichos von Chalkis (250-330 n.Chr.).
Die Schule der Pythagoreer (Sekte würden wir heute vielleicht sagen) wurde um 525 v.Chr.
gegründet und bestand zunächst aus ca. 500 Männern
und Frauen, deren Ziel es war, sich mit Philosophie, Mathematik, Musik,
Astronomie, Religion und Politik
zu befassen. Mathematische Erkenntnisse wurden bei Strafe nicht nach außen gegeben.
Deshalb ist nur wenig bekannt über deren Erkenntnisse. Der zu der Zeit schon
bekannt Satz des Pythagoras wurde immerhin bewiesen.
Sie hatten auch bewiesen, dass sich die Diagonale eines Quadrates nicht im
Verhältnis der Seiten ausdrücken lässt, das war im Prinzip die Entdeckung
der irrationalen Zahlen. Die Entdeckung passte nicht so recht in ihre Philosophie,
nach der die Natur sich über Verhältnisse natürlicher Zahlen erklären lassen müsse.
Zahlenspielereien betrieben sie vor allem in der Astronomie und Musik.
Die neuen Mitglieder des Bundes durften Pythagoras nicht sogleich sehen. Erst nach einer Probezeit hörten sie die Stimme des Meisters, der hinter einem Vorhang sprach, nach Jahren durften sie ihn sehen und mit ihm reden.
Die Stellung der Frau in diesem Bund ist bemerkenswert. Immerhin führten Pythagoras' Frau nach seinem Tod und später seine Tochter Damo den Bund. Es soll noch weitere bekannte Frauen bei den Pythagoreern gegeben haben.
Die pythagoreische Schule soll sehr bekannt gewesen sein, trotz ihrer Wissensabschottung nach außen. Viele strebten Mitgliedschaft an, nicht alle wurden aufgenommen, unter ihnen ein gewisser Kylon. Der soll zwanzig Jahre später Schuld am Tod des Pythagoras auf sich geladen haben und noch später für die Zerschlagung des Bundes verantwortlich gewesen sein.
siehe www.philosophenlexikon.de
Auf den Zahlenmystizismus der Pythagoreer geht die Beschäftigung mit allerlei
merkwürdigen Eigenschaften von Zahlen zurück. So nennt man
befreundete Zahlen oder soziale Zahlen, solche Zahlen, bei denen die Summe
ihrer echten Teiler und der 1 gerade die andere Zahl ergibt. Das kleinste solcher
Paare ist (220;284).
Teiler von 220: 1+2+4+5+10+11+20+22+44+55+110 = 284
Teiler von 284: 1+2+4+71+142 = 220.
Eine vollkommene Zahl ist mit sich selbst befreundet, z.B. die natürliche Zahl 6, weil
Teiler von 6: 1+2+3 = 6.
Die 28 ist auch so ein Kandidat, weil
1+2+7+14=28,
ebenso die 496, weil
1+2+4+8+16+31+62+124+248=496
und 8128, weil
1+2+4+8+16+32+64+127+254+508+1016+2032+4064=8128.
Es wird nicht leicht sein, weitere vollkommene Zahlen zu finden.
Das hat Euklid schon erledigt, indem er nachwies, dass
jede gerade Zahl der Form (2n - 1) · 2n-1
eine vollkommene Zahl ist, wenn 2n -1 eine Primzahl ist.
Für n = 2,3,5,7,13,19,31 ergeben sich die vollkommenen Zahlen
6, 28, 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128.
Auffallend: Die Zahlen sind alle gerade und enden auf 6 oder 28.
Sollte es auch ungerade vollkommene Zahlen geben, dann nicht kleiner als 1036.
Davon wussten die Pythagoreer noch nicht, das fanden viele Jahrhunderte später
der Mathematiker Leonhard Euler und der Pater Marin Mersenne.
Die Zahl Eins war den Pythagoreern keine eigentliche Zahl, vielmehr
hat sie am Anfang aller Zeiten, als das Chaos noch herrschte, alle weiteren Zahlen
hervorgebracht.Das korrespondiert bestens mit der griechischen Schöpfungsgeschichte:
Am Anfang der Zeiten war das Chaos, daraus wurde Gaia (Mutter Erde) geboren, die
ihren Sohn Kronos gebar, mit dem sie das Göttergeschlecht ... zeugte usw.
Die Zahl Drei hatte insofern eine besondere Bedeutung, als sie die erste Zahl war, die Anfang (1), Mitte (2) und Ende (3) hat, gleichzusetzen mit Geburt, Leben und Tod.

Dreieckszahlen
ergeben geometrisch angeordnet stets ein gleichseitiges Dreieck. Mag ja sein, dass
man sich daran erfreuen kann. Die Zahl Zehn war den Pythagoreern besonders
heilig, weil sie aus den ersten vier natürlichen Zahlen hervorgeht:
Die Zahl Sieben war den Pythagoreern Symbol der Krise, sofern die Überlieferungen stimmen. Na ja, ist ja auch eine Primzahl, wenn auch nicht die erste, vielleicht war ihr Schriftbild zu der Zeit besonders schön.

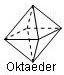
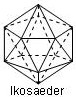
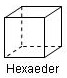
Regelmäßige Polyeder
haben als Oberfläche jeweils kongruente n-Ecke (n = 3; 4; 5), Tetraeder 4, Oktaeder 8, Ikosaeder 20 gleichseitige Dreiecke, Hexaeder 6 Quadrate, Dodekaeder 12 regelmäßige Fünfecke. Es kann nachweislich nicht mehr als fünf solcher Körper geben, die Pythagoreer kannten Tetraeder, Hexaeder, Oktaeder sowie Ikosaeder und verbanden sie mit den Griechen wichtigen Elementen der physikalischen Welt: Feuer, Erde, Luft und Wasser. Die Entdeckung des Dodekaeders brachte ihr Weltbild vorübergehend in eine Krise. Schließlich verbanden sie den neuen Körper mit dem Begriff des Universums, womit die Krise quasi auf höherer Ebene gelöst war.
Mehr dazu kann man lesen von Rolf Fraedrich in einer Broschüre
Lehrmittel aktuell des Schulbuchverlages Westermann, Heft 1, Februar 1993, einiges daraus
habe ich sinngemäß verwendet.