Inhalt
Beweise
Anfangs ist der unbedarfte Schüler natürlich geneigt, ein rechtwinkliges Dreieck
zu zeichnen, die Seitenlängen zu messen, mit dem Taschenrechner das gewünschte
Ergebnis zu ermitteln. Geübt durch den Physikunterricht, falls die Schulgesetzgebung
seines Landes solche fundamentale Wissensvermittlung erlaubt, wird er im
Rahmen der Messungeauigkeiten bald den Pythagoras bestätigt haben.
Der Hinweis auf die unendlich vielen anderen Dreiecke, die er noch zu bearbeiten
habe, wird die Einsicht fördern, dass es wohl besser sei, den Beweis
allgemein für alle Dreiecke zu führen.
Wenn zu diesem Zeitpunkt der Wissensvermittlung im Fach Mathe die Ähnlichkeitssätze schon behandelt wurden, dann wird der Lehrer diese Sätze als Voraussetzungen für seinen Beweis nutzen (können).

Drei zueinander ähnliche Dreiecke:
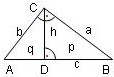
Winkel BCA
h ist Lot auf c
Dabei gilt:
(1) Dreick ABC ähnlich zu Dreieck BCD, weil rechter Winkel und Winkel ABC übereinstimmen
(2) Dreick ABC ähnlich zu Dreieck CAD, weil rechter Winkel und Winkel CAD übereinstimmen
(Hauptähnlichkeitssatz erfüllt, nämlich: Dreiecke sind ähnlich, wenn sie
in zwei Winkeln übereinstimmen)
(3) Damit sind auch Dreick BCD und Dreieck CAD zueinander ähnlich
(Wenn zwei Dreiecke einem dritten ähnlich sind, die kleinen dem großen, dann sind
sie auch untereinander ähnlich, die kleinen)
Umformen rechts stehender Gleichungen ergibt:
(1) a2=cp
(2) b2=cq
(3) h2=pq
Nun addieren wir Gleichung (1) und (2): a2+b2=c(p +q) Das ergibt:
(4) a2+b2=c2
(1) und (2) sind der Kathetensatz
(3) ist der Höhensatz
(4) ist der Satz des Pythagoras
Wir haben gleich drei Sätze bewiesen, das war schrecklich einfach. Vor allem wissen wir jetzt, diese Sätze gelten für alle rechtwinkligen Dreiecke. Aber wirklich nur für rechtwinklige Dreiecke.
Ach ja, konntet ihr Voraussetzung und Behauptung erkennen?
Wenn nicht, dann seht noch mal in die Satzgruppe hineien. Die Sätze beginnen
alle: In jedem rechtwinkligen Dreieck ist ...
Schreibt einfach: Wenn ein Dreick rechtwinklig ist, dann ...
In diese Form kann man mathematische Sätze eigentlich immer bringen:
Wenn Voraussetzung, dann Behauptung...
Über die Ähnlichkeitssätze ergeben sich folgende Gleichungen:
(1) a:c=p:a
(2) b:c=q:b
(3) h:q=p:h
Über den Kathetensatz, Gleichungen (1) und (2) wird der Satz des Pythagoras Gleichung (4) hergeleitet.