Inhalt
Pappus von Aleandria
Dieser Beweis geht vom allgemeinen Dreieck (ABC) aus.
Jetzt könntest du deine Tools für den Geometrieunterricht mal putzen,
dann funzt die folgende Konstruktion besser.
- Konstruiere an den Dreieckseiten (AC) und (BC) beliebige Parallelogramme.
Verlängere die Parallelogrammseiten (FD) und (GJ) derart, dass sie sich im Punkt S schneiden.
Verlängere die Strecke (SC), die Strecke (KY) werde = Strecke (SC).
Die Strecke (AB) verschiebe parallel durch den Punkt Y.
Die Gerade durch die Strecke (SC) verschiebe parallel durch die Punkte A und B.
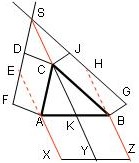
- Parallelogramm (ACDF) hat gleichen Flächeninhalt wie (ACSE), weil beide gleiche
Grundseite (AC) haben und gleiche Höhe, die du selbst findest.
Parallelogramm (ACSE) hat gleichen Flächeninhalt wie Parallelogramm (AXYK), weil gleiche Grundseite (SC) und gleiche Höhe, die du wieder finden sollst.
→ (ACDF) = (AXYK)
Die nächste Schlussfolgerung finde selbst.
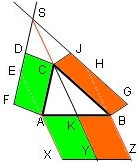
Vorsicht: Die Begriffe Hypothenuse und Kathete bleiben hier natürlich außen vor,
wir haben es mit einem allgemeinen Dreieck zu tun.
Aber wenn die Geschichte für allgemeine Dreiecke gilt...
Das rechtwinklige Dreieck ist ja nur ein Spezialfall des allgemeinen Dreieckes.
Pappus von Alexandria, ca. 300 v.Chr.