Inhalt
Quadrate
Bei diesem Beweis bedienen wir uns etwas ungewöhnlich zweier Quadrate.
Der gesamte Flächeninhalt ist
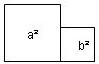
Nun zeichnen wir zwei rechtwinklige Dreiecke in die Ausgangsfigur entsprechend
der 2. Abbildung.
Der gesamte Flächeninhalt besteht aus 2 Dreiecken und einem Fünfeck, also
Die Flächeninhalte beider Figuren sind natürlich gleich groß, deshalb
- a2 + b2 = 2[(ab)/2] + A5
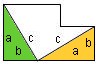
Die Dreiecke verschieben wir wie folgt
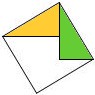
Das äußere Quadrat ist so groß wie die Summe aus den 2 Dreiecken und dem Fünfeck
- c2 = 2[(ab)/2] + A5
Die rechten Seiten der beiden Gleichungen sind gleich, also...