Inhalt
Sina Shiehyan
Im Kreis mit dem Mittelpunkt M sei die Strecke (AB) der Durchmesser,
C auf der Peripherie des Kreises, dann ist Dreieck (ABC) natürlich rechtwiklig bei C.
Durch Punkt C gehe die Tangente t, von A und B seien die Lote auf t gefällt.
Die Dreiecke (ABC), (ACQ) und (CBP) sind damit ähnlich zueinander,
die Begründung dafür könnt Ihr leicht selbst erbringen.
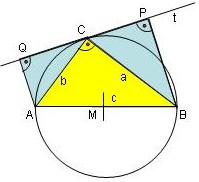
Wir addieren die Flächeninhalte der Dreiecke (ACQ) und (CBP)
- (ACQ) + (CBP) = (CQ)·(QA)/2 + (PC)·(PB)/2
- (ACQ) + (CBP) = ½ (PQ)·(QA)/2 + ½ (PQ)·(PB)/2
- (ACQ) + (CBP) = ½ {(PQ)·([(QA) + (PB)]/2)}
D.h.: Die Summe der Flächeninhalte der blau gefärbten Dreiecke ist halb so groß wie der Flächeninhalt des Trapezes (ABPQ).
Somit ist der Flächeninhalt des gelben Dreieckes (ABC) ist genau so groß wie die Summe der Flächeninhalte der blauen Dreiecke (ACQ) und (CBP).
Das führt unmittelbar zu unserer Gleichung für den Pythagoras.
Übrigens: Spiegelt das gelbe Dreieck mal an Strecke (AB) und seht dann auf Seite Verallgemeinerung
Dieser Beweis wurde von dem 14 jährigen Sina Shieyan aus Sahzevar, Iran an den Betreiber
der Seite http://www.cut-the-knot.org/pythagoras/index.shtml gesandt.
Dort findet man auch einen Link auf ein Faksimile des Originals dieses Beweises.
Die verwendete Figur wurde schon zuvor verwandt.