Inhalt

Michelle Watkins

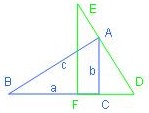
Gegeben sind die rechtwinkligen, zueinander kongruenten Dreiecke (ABC) und (DEF) entsprechend der Abbildung.
A liege auf der Strecke (DE), die Punkte B, F, C, D seien kollinear (liegen auf einer Geraden).
Es wird kein Problem sein nachzuweisen, dass Strecken (AB) und (DE) senkrecht zueinander sind.

Wir berechnen den Flächeninhalt des Dreieckes (BDE) auf zwei Wegen:

A₁ = (AB)·(DE)/2 bzw.
A₁ = c²/2

A₂ = (EF)·(BD)/2
A₂ = (EF)·[(BC) + (CD)]/2 = a·[a + (CD)]/2
Wir ersetzen (CD) = b²/a über den Strahlensatz, das kannst du selbst prüfen und erhalten
A₂ = a·[a + b²/a]/2 bzw.
A₂ = (a² + b²)/2

Natürlich ist A₁ = A₂ und deshalb...