Inhalt
Beweis nach Leonardo da Vinci
Das rechtwinklige Dreieck mit den Seitenlängen a,b,c und die braunen Quadrate bilden die übliche Pythagorasfigur, ergänzt durch zwei Dreiecke, die zum ersten kongruent sind.
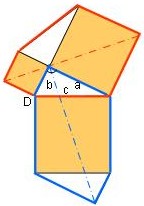
Das rot umrandete Sechseck wird durch die rote strichpunktierte Symmetrieachse
(axiale Symmetrie) in zwei kongruente Vierecke geteilt. Das blau umrandete Sechseck
wird durch die blaue strichpunktierte Symmetrieachse (radiale Symmetrie) in zwei flächengleiche
Vierecke geteilt.
Die untere Hälfte des roten Sechseckes, also das Viereck, wird um 90° nach rechts
um den Punkt D gedreht. Man erkennt, das rote Viereck ist kongruent zum blauen Viereck.
Der bloße Anschein genügt nicht, aber er hilft, einander entsprechende Strecken
und Winkel zu finden.
Folglich sind rotes und blaues Sechseck von gleicher Größe.
Zugegeben, das ist etwas verwirrend. Konstruiere einfach die Figur, schneide die
untere Hälfte des roten Sechseckes aus und experimentiere ausnahmsweise.
Subtrahieren wir vom roten Sechseck die zwei kongruenten Dreiecke, dann bleiben
die Kathetenquadrate übrig. Machen wir das beim blauen Sechseck, dann bleibt das
Hypothenusenquadrat übrig und zwar von gleicher Größe wie die Summe der Kathetenquadrate.
Schreibe die entsprechenden Gleichungen auf, es ist ganz einfach.