Inhalt

Inkreis1

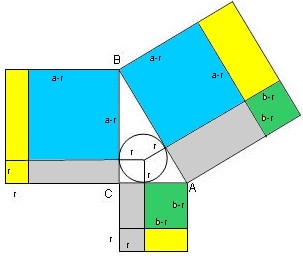
Wir gehen von der üblichen Pythagorasfigur aus und konstruieren den Inkreis. Die senkrecht auf den Dreiecksseiten stehenden Inkreisradien verlängern wir wie in der Abbildung. Wie wir zu den einzelnen Quadraten und Rechtecken im Hypothenusenquadrat und den Kathetenquadraten kommen, das erkennt ihr selbst.
Die Figur sieht so schön aus, dass ihr sie unbedingt konstruieren solltet.

Blaues und grünes Quadrat in den Kathetenquadraten finden sich im Hypothenusenquadrat wieder.
Wir werden zeigen, dass die Summe der gelben Flächen in den Kathetenquadraten gleich dem gelben Rechteck im Hypothenusenquadrat ist.
Wenn wir das mit gelb schaffen, dann mit grau allemal.

Wir betrachten unten in der linken Figur wieder unser Dreieck (ABC) mit dem Inkreis, zusätzlich zwei Winkelhalbierende. Ihr werdet herausfinden, warum die zwei Dreiecke links oben und die zwei Dreiecke rechts unten jeweils kongruent sind.
Also können wir das linke Rechteck in das rechte überführen.

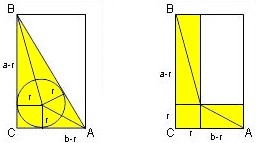
Weil das linke weiße Dreieck den Flächeninhalt ab/2 hat, muss das rechte weiße Rechteck ebenfalls den Flächeninhalt (a - r)(b - r) = ab/2 haben, die Summe der farbigen Flächen im rechten Rechteck natürlich auch: r(a - r) + r(b - r) + r² = ab/2

Nun vergleicht noch die gelben Flächen in der oberen Abbildung mit den Flächen im rechten Rechteck der unteren Abblidung. Ach so, die grauen aus der oberen Abbildung auch noch. Alles klar?

Inkreis
schneidet die Dreiecksseiten jeweils in einem Punkt.
Sein Mittelpunkt = Schnittpunkt der Winkelhalbierenden.