Inhalt
Sekantentangentensatz1
Nach o.g. Satz gilt:
(BC)2 = (BE) · (BD)
In Worten: Jede Tangente von einem Punkt an einem Kreis ist mittlere
Proportionale an den durch den Kreis gebildeten zugehörigen Sekantenabschnitten.
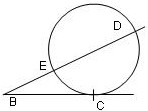
Dieser Satz lässt sich bestens benutzen, um den Pythagoras zu beweisen. Wir modifizieren obige Figur und benennen die Dreiecksseiten:
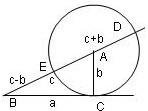
A ist Mittelpunkt des Kreises
(AB) = c ist Hypothenuse des Dreieckes (ABC)
a;b sind die Katheten, rechter Winkel bei C
(BC) = a ist Tangente
(BE) = c -b und (BD) = c + b sind Sekantenabschnitte
Unseren obigen Satz darauf angewandt ergibt die Beziehung
a2 = (c - b)(c + b)
Ausrechnen könnt ihr selbst, um wieder den Pythagoras zu erhalten.
Begriffe am Kreis
