Inhalt

Ann Condit

Wir gehen wieder aus vom rechtwinkligen Dreieck ABC, rechter Winkel bei C. Dazu zeichnen wir die üblichen Kathetenquadrate, die entstandenen Punkte P und Q werden verbunden. So entsteht Dreieck QPC, das kongruent ist zum Dreieck ABC nach dem Kongruenzsatz SWS.
Srecke (MC) ist Seitenhalbierende der Hypothenuse (AB), sie schneidet die Hypothenuse (QP) in R.
Nun müssen wir nachweisen, Strecke (MR) ist senkrecht zu Strecke (PQ):
Dreieck BCM ist gleichschenklig, weil Strecke (MC) Seitenhalbierende von (AB) ist und Winkel (BCA) = 90⁰. Winkel (BCM) und (PCR) sind kongruente Scheitelwinkel.
Winkel (CAM) und(QPC) sind kongruent wegen der Dreiecke (ABC) und (QPC).
Die Rolle des Winkels (CMS) könntest du noch klären,
dann wissen wir, warum Strecke (MR) senkrecht zu (PQ) ist.
Ziemlich viele Vorbemerkungen waren das.

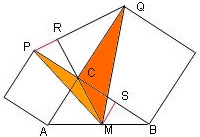
Betrachte das braune Dreieck (MCP):
Höhe auf der Strecke (PC) = b ist (MS) = (AC)/2, wegen (AC) = b auch (MS) = b/2.
Flächeninhalt braunes Dreieck: A_braun1 = b²/4
Nun sei (PR) Höhe auf (MC) = c/2, dann folgt
Flächeninhalt braunes Dreieck: A_braun2 = c·(PR)/4

Nun das rote Dreieck (QCM):
Höhe auf der Strecke (QC) ist (CS) = a/2
Flächeninhalt rotes Dreieck: A_rot1 = a²/4
Nun sei (QR) Höhe auf (MC) = c/2, dann folgt
Flächeninhalt rotes Dreieck: A_rot2 = c·(QR)/4

Natürlich ergibt
A_braun1 + A_rot1 = A_braun2 + A_rot2
b²/4 + a²/4 = c·(PR)/4 + c·(QR)/4
Die ganze Sache mit 4 multiplizieren, c ausklammern, (PR) + (QR) = c beachten, erledigt.