Inhalt

Zerlegung

Das rechtwinklige Dreieck ABC werde viermal so angeordnet wie in der Abbildung

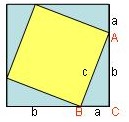
Flächeninhalt äußeres Quadrat (a + b)²
Inneres Quadrat plus vier kongruente Dreiecke c² + 4·(ab)/2
Das setzen wir gleich

(a + b)² = c² + 4·(ab)/2

a² + 2·ab + b² = c² + 2·ab
a² + b² = c²

Ordnen wir die vier Dreiecke anders an

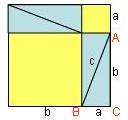
Flächeninhalt äußeres Quadrat (a + b)²
Innen 4 Dreiecke plus 2 Quadrate [4·(ab)/2] + a² + b²
Gleichsetzen und lösen kannst du selbst

Nun betrachten wir obige Abbildungen nebeneinander:
Die äußeren Quadrate sind gleich groß, die vier Dreiecke auch,
also folgt unmittelbar

c2 =

a2 + b2