Inhalt
Sekantentangentensatz2
Wir bemühen den o.g. Satz noch einmal zum Beweis des Pythagoras.
Dazu betrachten wir zunächst folgende Figur:
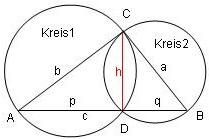
(ABC) ist das rechtwinklige Dreieck, rechter Winkel bei C
(AC) = b = Durchmesser von Kreis1
(BC) = a = Durchmesser von Kreis2
Hypothenuse c = p + q
Dreieck (CAD) = rechtwinklig (Thaleskreis), D auf c
Dreieck (BCD) = rechtwinklig (Thaleskreis), D auf c
Nun wenden wir unseren o.g. Satz an:
(AC) = b ist Tangente am Kreis2,
(AD) = p und (AB) = c sind die Sekantenabschnitte am Kreis2
Folglich gilt
- b2 = pc
(BC) = a ist Tangente am Kreis1
(BD) = q und (BA) = c sind die Sekantenabschnitte am Kreis1
Folglich gilt
- a2 = qc
Wir addieren beide Gleichungen
- a2 + b2 = qc + pc
Der Rest ist euch bereits klar.