Inhalt

Inkreis2

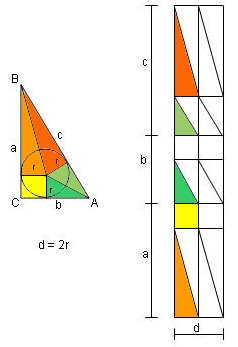
Wir gehen wieder aus vom rechtwinkligen Dreieck (ABC), rechter winkel bei C, Inkreisradius r. Um die Sache besser zu übersehen, zeichnen wir zwei Winkelhalbierende in das Dreieck.
Daneben zeichnen wir das Rechteck mit dem Flächeninhalt A_R = d (a + b + c)
Farblich unterschiedene Teilflächen im Dreieck finden sich wieder im Rechteck.
Ihr werdet erkennen, dass der Flächeninhalt des Dreieckes viermal im Flächeninhalt des Rechteckes zu finden ist, also A_R = 4·A_D

Am Dreieck (ABC) erkennt man
(a - r) + (b - r) = c, umgewandelt
a + b = c + 2r bzw.
a + b = c + d.
Deshalb haben die folgenden Rechtecke gleiche Flächeninhalte
(a + b + c)·(a + b) = (a + b + c)·(c + d).

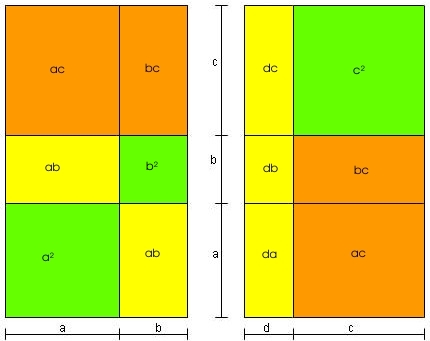
Links finden wir (braun) ac + bc, rechts auch.
Links finden wir (gelb) 2ab = 4·A_D, weiter oben hatten wir schon festgestellt d(a + b + c) = 4·A_D (gelb, rechts).
Somit bleibt nur a² + b² = c²