Inhalt
Tabit ibn Quora
Das beliebige Dreieck (ABC) habe bei C den Winkel γ≠90°.
Genau dieser Winkel trete im Dreieck (AEC) bei E auf,
im Dreieck (DBC) bei D. (c = d + e + f)
Die genannten 3 Dreiecke sind nach dem Hauptähnlichkeitssatz zueinander ähnlich.
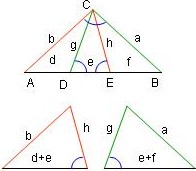
Daher gelten die Verhältnisgleichungen
- b/c = (d + e)/b → b2 = c(d + e)
a/c = (e + f)/a → a2 = c(e + f)
- a2 + b2 = c(d + 2e f)
Dieser Beweis ist allgemeiner als der auf der Seite Ähnlichkeit,
weil er vom allgemeinen Dreieck ausgeht und das rechtwinklige Dreieck als Sonderfall
enthält.
Tabit ibn Quora (836-901).
Tabit ibn Quora (836-901).