Inhalt

Beweis nach Bhaskara

Das rechtwinklige Dreieck mit den Seitenlängen a,b,c sei viermal so angeordnet wie in der Abbildung, dann ergibt sich das äußere Quadrat mit der Seitenlänge c und das innere Quadrat mit der Seitenlänge (b - a).
Weise nach, dass wirklich zwei Quadrate entstanden sind.

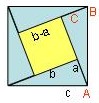
Der Flächeninhalt des äußeren Quadrates ist genauso groß wie die Summe aus dem inneren Quadrat und den vier rechtwikligen Dreiecken:

c² = (b - a)² + 4 · (ab)/2
c² = b² - 2ab + a² + 2ab
c² = a² + b²