Inhalt
Beweis durch Flächenzerlegung
Jede auftretende Strecke ist zu einer Quadratseite parallel.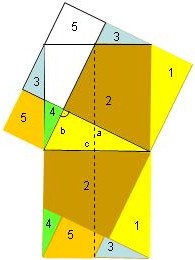
Das rechtwinklige Dreieck mit den Seiten a,b,c sowie die Pythagorasfigur, ergänzt links oben um ein Rechteck, sollte trotz des Farbenwirrwarrs zu erkennen sein. Die Teilflächen 1 bis 5 im Hypothenusenquadrat finden sich in den Kathetenquadraten wieder. Also muss nachgewiesen werden, dass die einzelnen Teilflächen 1 bis 5 zueinander kongruent sind.
Die Dreiecke 1 haben die Seiten a und c gemeinsam, außerdem den spitzen Winkel
(Scheitelwinkel) an der Ecke, an der sie sich schneiden.
Die Vierecke 2 haben die Seiten a und c gemeinsam (erkennbar, wenn man die anliegenden gelben
Dreiecke betrachtet) sowie in jeweils zwei rechten Winkeln. Betrachtet man die
Winkel der Vierecke 2 zwischen ihren Seiten a und c, dann erkennt man, dass auch sie
übereinstimmen (dazu betrachtet man zunächst die rechten Winkel, die sich ergeben,
wenn man das ursprüngliche rechtwinklige Dreieck (a,b,c) und jeweils eines der Vierecke
betrachtet und den spitzen Winkel des Dreieckes subtrahiert). Da die Kongruenzsätze
für Dreiecke gelten, muss man noch die Diagonalen in den Vierecken 2 betrachten
Wegen der gestrichelten schwarzen Linie haben die blauen Dreiecke 3 die größere Seite gemeinsam,
außerdem besitzen beide einen rechten Winkel. Einen zweiten gemeinsamen Winkel
kann man leicht nachweisen
Zwei kongruente Winkel in den Dreiecken 4 zu finden dürfte der vielen Parallelen wegen
kein Problem sein. Damit wären die Dreiecke erst ähnlich, also brauchen wir noch eine
kongruente Seite. Die finden wir, wenn wir die größere der beiden Katheten von Dreieck 4
betrachten, die ist so groß wie b im Ausgangsdreieck (a,b,c).
Die Vierecke 5 stimmen in ihrer kleineren Seite mit der kleineren Kathete von Dreieck 3
überein, in einer anderen mit der größeren Kathete von Dreieck 4. Ferner haben beide Vierecke
jeweils zwei rechte Winkel. Es ist leicht, einen dritten Winkel als übereinstimmend
zu erkennen, damit stimmen sie in 4 Winkeln überein. Für die Kongruenz reicht das,
wenn wir noch die Diagonalen einbeziehen wegen der Kongruenzsätze für Dreieck.