Inhalt

Perigal

Gegeben ist die schon übliche Pythagorasfigur, zeichne sie. Konstruiere den Mittelpunkt M des Quadrates mit der Seitenlänge a. Verschiebe die Dreiecksseite c durch den Mittelpunkt M derart, dass die Quadratseiten wie in der Abbildung geschnitten werden. Konstruiere die Senkrechte zu c und verschiebe die auch durch M mit voriger Nebenbedingung. Mit der Schere schnippelst du die 4 entstandenen Vierecke aus, ebenso das Quadrat über b. Wenn du die Schnipsel in das Quadrat über c legst, dann hast du einen Erkenntnisgewinn.

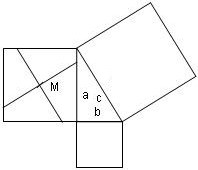
Perigal1

Wenn du mit einem halbwegs ordentlichen Grafikprogramm umgehst, dann kannst du die Arbeit mit der Schere sparen.Aber es wäre okay, wenn du mal so eine schöne Konstruktion nach allen Regeln der Kunst durchführst.
Mit dem Rechner sieht das z.B. so aus:

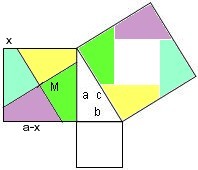
Perigal2

Natürlich geht es wieder um c2 = a2 + b2, und das ist grafisch beinahe überzeugend.

Rechnerisch müssen wir die Sache noch lösen.
Dazu betrachten wir das blaue und pinkfarbene Viereck links im Kathetenquadrat über a, sie bilden zusammen ein Trapez. Sein Flächeninhalt ist:

    a·[(a-x)+x]/2 = a2/2
Das multiplizieren wir mit 2, weil wir zwei Trapeze haben, schließlich noch +b2, und wir erhalten c2

Es ist erstaunlich, wer sich alles mit Beweisen zum Satz des Pythagoras befasst hat. In diesem Fall war es Henri Perigal (1801-1898), ein Börsenmakler in London. Der Beweis wird auch Schaufelradbeweis genannt, na ja...